Motor Control with Arduino: A Case Study in Data-Driven Modeling and Control Design
By Pravallika Vinnakota, MathWorks
Tuning a controller on a physical prototype or plant hardware can lead to unsafe operating conditions and damage the hardware. A more reliable approach is to build a plant model and simulate it to verify the controller at different operating conditions so as to run what-if scenarios without risk.
When first-principles modeling is not feasible, an alternative is to develop models from input-output measurements of the plant. A low-order, linear model might be sufficient for designing a basic controller. Detailed analysis and design of a higher-performance controller requires a higher-fidelity and possibly nonlinear model.
Using a simple control system for a DC motor as an example, this article shows how to identify a plant model from input-output data, use the identified model to design a controller, and implement it. The workflow includes the following steps: acquiring data, identifying linear and nonlinear plant models, designing and simulating feedback controllers, and implementing these controllers on an embedded microprocessor for real-time testing.
The models and scripts used in this example are available for download.
The DC Motor: Control Design Goals
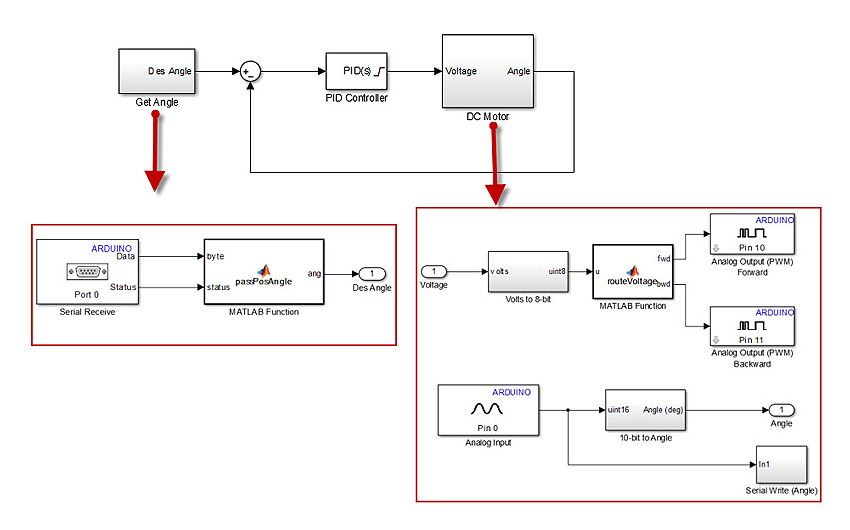
The physical system is a DC motor connected to an Arduino® Uno board via a motor driver (Figure 1). We want to design a feedback controller for this motor to track a reference position. The controller will generate the appropriate voltage command based on the motor position reference data. When applied to the motor, this voltage will cause the motor to generate the torque that turns the motor shaft. We will use a potentiometer to measure the angle of rotation of the motor shaft, and feed this angle back to the controller.
The motor driver integrated circuit (IC) increases the current capability and can drive the motor in both directions. We receive the motor position data through an Analog Input pin on the Arduino board and compute the error between the reference and actual data (the controller input). We send a voltage command (the controller output) to two Analog Output pins on the board as PWM signals. These signals are fed to the driver IC that provides the motor with the appropriate drive currents.
The controller must keep the system stable and provide fast reference tracking with minimal steady-state error and overshoot.
Acquiring and Processing Data
We connect the host PC to the Arduino board using a Simulink® capability that lets you generate an executable and run it on selected hardware. Figure 2 shows the Simulink library for use with Arduino hardware.
To collect the data, the Arduino board will send voltage commands to the motor and measure the resulting motor angles. We create a Simulink model to enable data collection. The host machine must communicate with the Arduino board to send voltage commands and receive back the angle data. We create a second model to enable this communication.
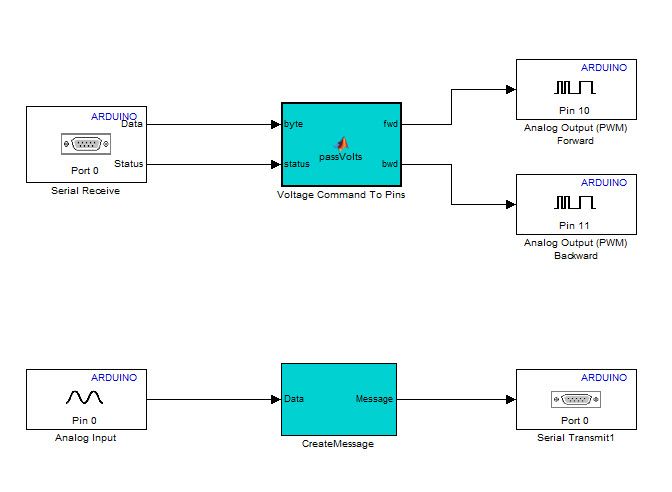
In the model that will run on the Arduino Uno board (Figure 3), the MATLAB® Function block Voltage Command To Pins reads from the serial port and routes the voltage commands to the appropriate pins. We use serial communication protocol to enable the host computer to communicate with the Arduino board. In the CreateMessage subsystem, a complete serial message is generated from the motor position data obtained from one of the analog input pins on the board.
We create a real-time application from the model by selecting Tools > Run on Target Hardware > Run. We are then ready to acquire the input/output data using the model that will run on the host computer (Figure 4).
We send various voltage profiles to excite the system, and record and log the corresponding position data. At the end of the simulation, the signal logging feature in Simulink will create a Simulink data set object in the workspace containing all the logged signals as time-series objects.
Next, we prepare the collected data for estimation and validation. Using the following commands, we convert the data into iddata objects for import into the System Identification Tool in System Identification Toolbox™.
>> logsout
logsout =
Simulink.SimulationData.Dataset
Package: Simulink.SimulationData
Characteristics:
Name: 'logsout'
Total Elements: 2
Elements:
1: 'Voltage'
2: 'Angle'
-Use getElement to access elements by index or name.
-Use addElement or setElement to add or modify elements.
Methods, Superclasses
>> u = logsout.getElement(1).Values.Data;
>> y = logsout.getElement(2).Values.Data;
>> bounds1 = iddata(y,u,0.01,'InputName','Voltage','OutputName','Angle',...
...'InputUnit','V','OutputUnit','deg')
Time domain data set with 1001 samples.
Sample time: 0.01 seconds
Outputs Unit (if specified)
Angle deg
Inputs Unit (if specified)
Voltage V
We will be working with 12 data sets. These data sets were selected to ensure adequate excitation of the system and to provide sufficient data for model validation.
Developing Plant Models from Experimental Data
Developing plant models using system identification techniques involves a tradeoff between model fidelity and modeling effort. The more accurate the model, the higher the cost in terms of effort and computational time. The goal is to find the simplest model that will adequately capture the dynamics of the system.
We follow the typical workflow for system identification: We start by estimating a simple linear system and then estimate a more detailed nonlinear model that is a more accurate representation of the motor and captures the nonlinear behavior. While a linear model might suffice for most controller design applications, a nonlinear model enables more accurate simulations of the system behavior and controller design over a range of operating points.
Linear System Identification
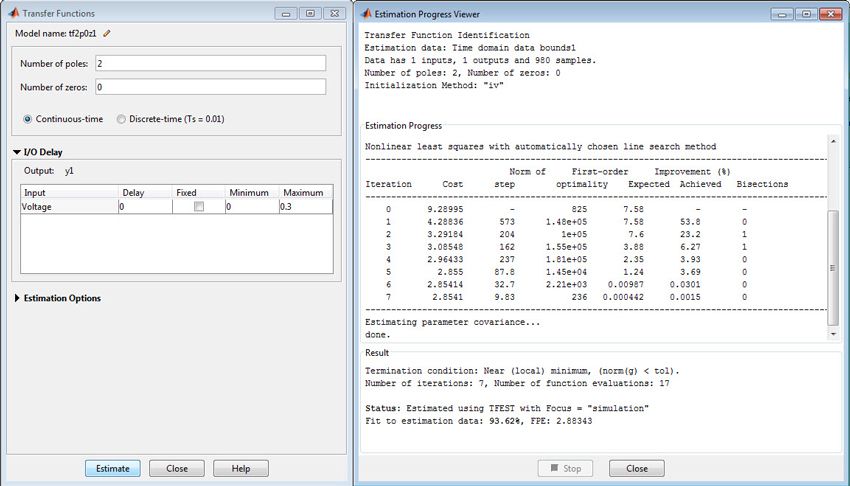
Using the iddata objects, we first estimate a linear dynamic model for the plant as a continuous-time transfer function. For this estimation, we specify the number of poles and zeros. System Identification Toolbox then automatically determines their locations to maximize the fit to the selected data sets.
We launch the System Identification Tool by executing
>> ident
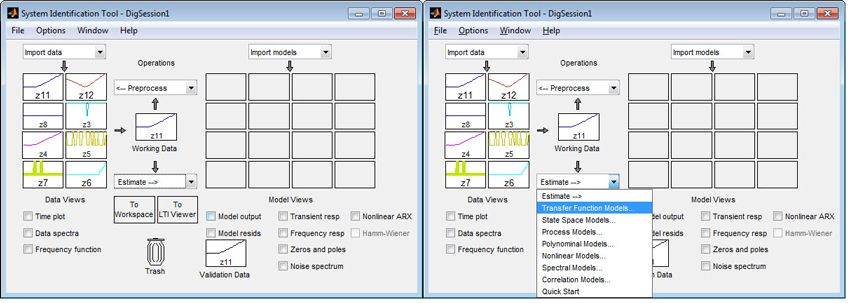
We can import the data sets into the tool from the base workspace using the Import Data pull-down menu (Figure 5). We also have the option to preprocess the imported data. To start the estimation process, we select the working data that will be used to estimate a model and the validation data against which the estimated model will be tested. We can use the same data set for both estimation and validation initially, and then use other data sets to confirm our results. Figure 5 shows the System Identification Tool with the data set imported. The estimation data set, data set 11, comes from an experiment designed to avoid exciting nonlinearities in the system.
We can now estimate a continuous transfer function for this data. In our example, we estimate a 2-pole, no-zero, continuous-time transfer function (Figure 6).
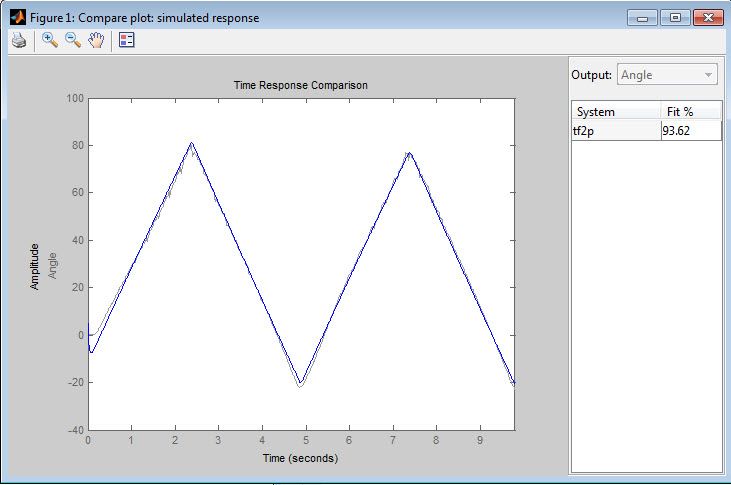
We compare the simulation response of the estimated model against measured data by checking the Model Output box in the System Identification Tool. The fit between the response of the estimated linear model and the estimation data is 93.62% (Figure 7).
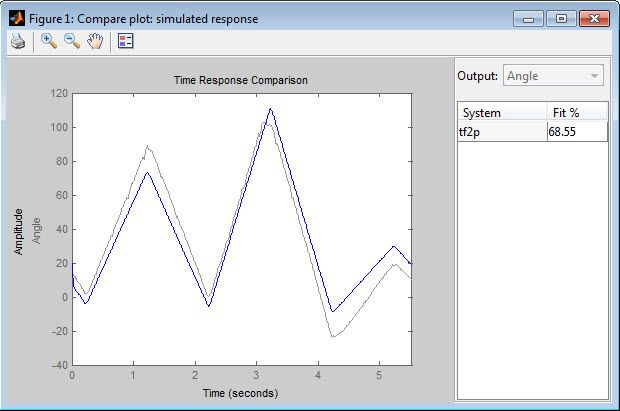
To ensure that the estimated transfer function represents the motor dynamics, we must validate it against an independent data set. For this purpose we select data set 12, where the motor operates linearly as our validation data. We achieve a reasonably accurate fit (Figure 8).
While the fit is not perfect, the transfer function that we identified does a good job of capturing the dynamics of the system. We can use this transfer function to design a controller for the system.
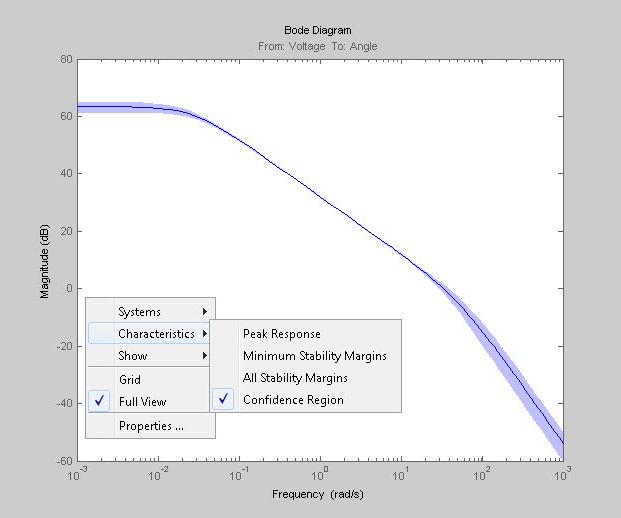
We can also analyze the effect of plant uncertainty. Models obtained with System Identification Toolbox contain information not only about the nominal parameter values but also about parameter uncertainty encapsulated by the parameter covariance matrix. A measure of the reliability of the model, the computed uncertainty is influenced by external disturbances affecting the system, unmodeled dynamics, and the amount of collected data. We can visualize the uncertainty by plotting its effect on the model’s response. For example, we can generate the Bode plot of the estimated transfer function showing 1 standard deviation confidence bound around the nominal response (Figure 9).
Nonlinear System Identification
A linear model of the motor dynamics, created by using data collected from a linear region of its operation, is useful for designing an effective controller. However, this plant model cannot capture nonlinear behavior exhibited by the motor. For example, data set 2 shows that the motor’s response saturates at about 100°, and data set 3 shows that the motor is not responsive to small command voltages, perhaps owing to dry friction.
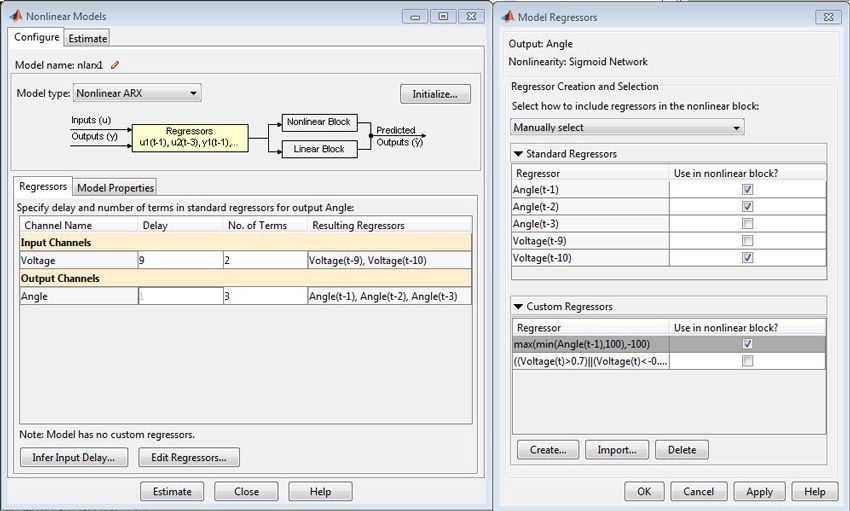
In this step, we will create a higher-fidelity model of the DC motor. To do that, we estimate a nonlinear model for the DC motor. A closer inspection of the data reveals that the change in the slope of the response is not linearly related to the change in voltage. This trend suggests nonlinear, hysteresis-like behavior. Nonlinear ARX (NLARX) models offer considerable flexibility, enabling us to capture such behavior using a rich set of nonlinear functions, such as wavelets and sigmoid networks. Furthermore, these models let us incorporate what we have discovered about the system nonlinearities using custom regressors.
For the NLARX modeling to be effective, we need data that is rich in information about the nonlinearities. We merge three data sets to create the estimation data. We merge five other data sets to create a larger, multi-experiment, validation data set.
>> mergedD = merge(z7,z3,z6)
Time domain data set containing 3 experiments.
Experiment Samples Sample Time
Exp1 5480 0.01
Exp2 980 0.01
Exp3 980 0.01
Outputs Unit (if specified)
Angle deg
Inputs Unit (if specified)
Voltage V
>> mergedV = merge(z1,z2,z4,z5,z8);
The nonlinear model had various adjustable components. We adjusted the model orders, delays, type of nonlinear function, and the number of units in the nonlinear function. We added regressors that represent saturation and dead-zone behavior. After several iterations, we chose a model structure that employed a sigmoid network with a parallel linear function and used a subset of regressors as its inputs. The parameters of this model were estimated to achieve the best possible simulation results (Figure 10).
The resulting model has an excellent fit of >90% for the estimation data as well as for the validation data. This model can be used for controller design as well as for analysis and prediction.
Designing the Controller
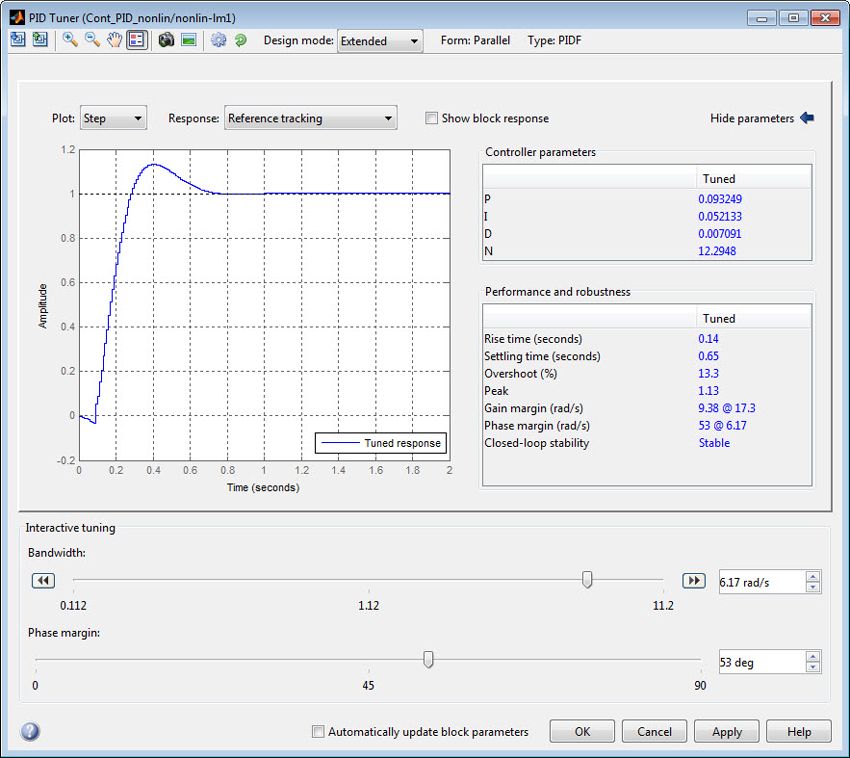
We are now ready to design a PID controller for the higher-fidelity nonlinear model. We linearize the estimated nonlinear model at an operating point of interest and then design a controller for this linearized model.
We tune the PID controller and then select its parameters (Figure 11).
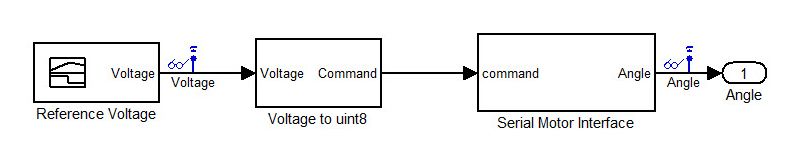
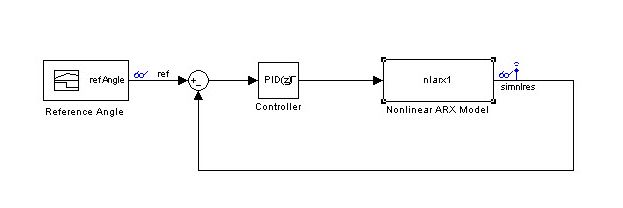
We also check how this controller performs on the nonlinear model. Figure 12 shows the Simulink model that we use to obtain the simulation response of the nonlinear ARX model.
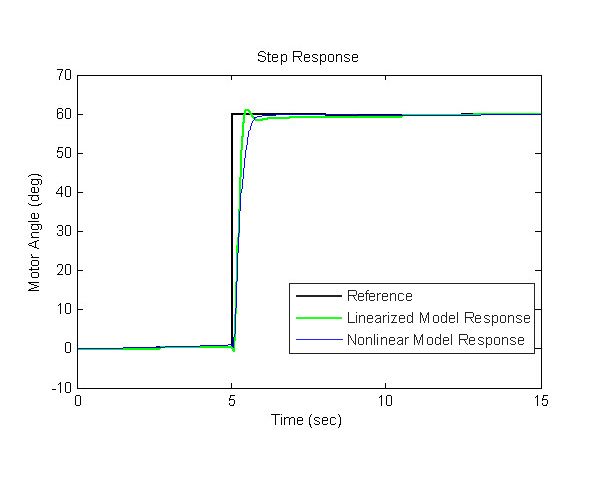
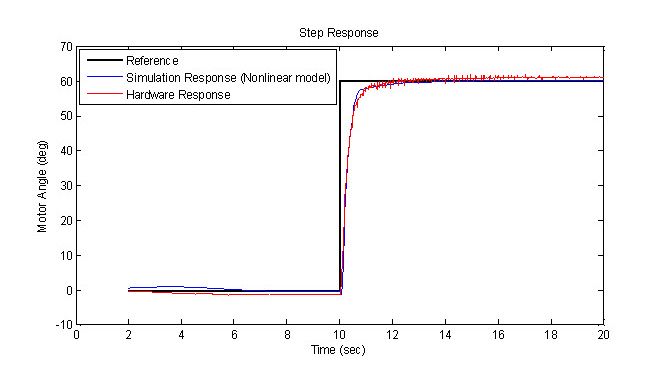
We then compare the linearized and nonlinear model closed-loop step responses for a desired reference position of 60° (Figure 13).
Testing the Controller on Hardware
We create a Simulink model with the controller and place it on the Arduino Uno board using Simulink built-in support for deploying models to target hardware (Figure 14).
We designed a controller by linearizing the estimated nonlinear ARX model about a certain operating point. The results for this controller show that the hardware response is quite close to the simulation results (Figure 15).
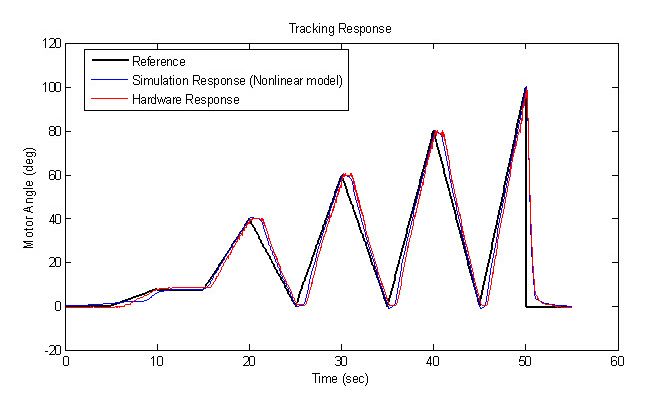
We also tested how well the controller tracks a random reference command. We see that the hardware tracking performance is also very close to that obtained during simulation (Figure 16).
This example, while simple, captures the essential steps for data-driven control. We collected input/output data from a given hardware target and used System Identification Toolbox to construct models of the system. We showed how you can create models of lower and higher fidelity and design controllers using these estimated models. We then verified the performance of our controllers on the actual hardware.
Published 2013 - 92066v00