pdist2
Pairwise distance between two sets of observations
Syntax
Description
D = pdist2(X,Y,Distance,DistParameter)Distance and
DistParameter. You can specify
DistParameter only when Distance is
'seuclidean', 'minkowski', or
'mahalanobis'.
D = pdist2(___,Name,Value)
D = pdist2(X,Y,Distance,'Smallest',K)computes the distance using the metric specified byDistanceand returns theKsmallest pairwise distances to observations inXfor each observation inYin ascending order.D = pdist2(X,Y,Distance,DistParameter,'Largest',K)computes the distance using the metric specified byDistanceandDistParameterand returns theKlargest pairwise distances in descending order.
Examples
Compute Euclidean Distance
Create two matrices with three observations and two variables.
rng('default') % For reproducibility X = rand(3,2); Y = rand(3,2);
Compute the Euclidean distance. The default value of the input argument Distance is 'euclidean'. When computing the Euclidean distance without using a name-value pair argument, you do not need to specify Distance.
D = pdist2(X,Y)
D = 3×3
0.5387 0.8018 0.1538
0.7100 0.5951 0.3422
0.8805 0.4242 1.2050
D(i,j) corresponds to the pairwise distance between observation i in X and observation j in Y.
Compute Minkowski Distance
Create two matrices with three observations and two variables.
rng('default') % For reproducibility X = rand(3,2); Y = rand(3,2);
Compute the Minkowski distance with the default exponent 2.
D1 = pdist2(X,Y,'minkowski')D1 = 3×3
0.5387 0.8018 0.1538
0.7100 0.5951 0.3422
0.8805 0.4242 1.2050
Compute the Minkowski distance with an exponent of 1, which is equal to the city block distance.
D2 = pdist2(X,Y,'minkowski',1)D2 = 3×3
0.5877 1.0236 0.2000
0.9598 0.8337 0.3899
1.0189 0.4800 1.7036
D3 = pdist2(X,Y,'cityblock')D3 = 3×3
0.5877 1.0236 0.2000
0.9598 0.8337 0.3899
1.0189 0.4800 1.7036
Find the Two Smallest Pairwise Distances
Create two matrices with three observations and two variables.
rng('default') % For reproducibility X = rand(3,2); Y = rand(3,2);
Find the two smallest pairwise Euclidean distances to observations in X for each observation in Y.
[D,I] = pdist2(X,Y,'euclidean','Smallest',2)
D = 2×3
0.5387 0.4242 0.1538
0.7100 0.5951 0.3422
I = 2×3
1 3 1
2 2 2
For each observation in Y, pdist2 finds the two smallest distances by computing and comparing the distance values to all the observations in X. The function then sorts the distances in each column of D in ascending order. I contains the indices of the observations in X corresponding to the distances in D.
Accelerate Distance Computation Using fasteuclidean Distance
Create two large matrices of points, and then measure the time used by pdist2 with the default "euclidean" distance metric.
rng default % For reproducibility N = 10000; X = randn(N,1000); Y = randn(N,1000); D = pdist2(X,Y); % Warm up function for more reliable timing information tic D = pdist2(X,Y); standard = toc
standard = 7.8404
Next, measure the time used by pdist2 with the "fasteuclidean" distance metric. Specify a cache size of 100.
D = pdist2(X,Y,"fasteuclidean",CacheSize=100); % Warm up function tic D2 = pdist2(X,Y,"fasteuclidean",CacheSize=100); accelerated = toc
accelerated = 1.4593
Evaluate how many times faster the accelerated computation is compared to the standard.
standard/accelerated
ans = 5.3726
The accelerated version is more than twice as fast for this example.
Compute Pairwise Distance with Missing Elements Using a Custom Distance Function
Define a custom distance function that ignores coordinates with NaN values, and compute pairwise distance by using the custom distance function.
Create two matrices with three observations and three variables.
rng('default') % For reproducibility X = rand(3,3) Y = [X(:,1:2) rand(3,1)]
X =
0.8147 0.9134 0.2785
0.9058 0.6324 0.5469
0.1270 0.0975 0.9575
Y =
0.8147 0.9134 0.9649
0.9058 0.6324 0.1576
0.1270 0.0975 0.9706
The first two columns of X and Y are identical. Assume that X(1,1) is missing.
X(1,1) = NaN
X =
NaN 0.9134 0.2785
0.9058 0.6324 0.5469
0.1270 0.0975 0.9575
Compute the Hamming distance.
D1 = pdist2(X,Y,'hamming')
D1 =
NaN NaN NaN
1.0000 0.3333 1.0000
1.0000 1.0000 0.3333
If observation i in X or observation j in Y contains NaN values, the function pdist2 returns NaN for the pairwise distance between i and j. Therefore, D1(1,1), D1(1,2), and D1(1,3) are NaN values.
Define a custom distance function nanhamdist that ignores coordinates with NaN values and computes the Hamming distance. When working with a large number of observations, you can compute the distance more quickly by looping over coordinates of the data.
function D2 = nanhamdist(XI,XJ) %NANHAMDIST Hamming distance ignoring coordinates with NaNs [m,p] = size(XJ); nesum = zeros(m,1); pstar = zeros(m,1); for q = 1:p notnan = ~(isnan(XI(q)) | isnan(XJ(:,q))); nesum = nesum + ((XI(q) ~= XJ(:,q)) & notnan); pstar = pstar + notnan; end D2 = nesum./pstar;
Compute the distance with nanhamdist by passing the function handle as an input argument of pdist2.
D2 = pdist2(X,Y,@nanhamdist)
D2 =
0.5000 1.0000 1.0000
1.0000 0.3333 1.0000
1.0000 1.0000 0.3333
Assign New Data to Existing Clusters and Generate C/C++ Code
kmeans performs k-means clustering to partition data into k clusters. When you have a new data set to cluster, you can create new clusters that include the existing data and the new data by using kmeans. The kmeans function supports C/C++ code generation, so you can generate code that accepts training data and returns clustering results, and then deploy the code to a device. In this workflow, you must pass training data, which can be of considerable size. To save memory on the device, you can separate training and prediction by using kmeans and pdist2, respectively.
Use kmeans to create clusters in MATLAB® and use pdist2 in the generated code to assign new data to existing clusters. For code generation, define an entry-point function that accepts the cluster centroid positions and the new data set, and returns the index of the nearest cluster. Then, generate code for the entry-point function.
Generating C/C++ code requires MATLAB® Coder™.
Perform k-Means Clustering
Generate a training data set using three distributions.
rng('default') % For reproducibility X = [randn(100,2)*0.75+ones(100,2); randn(100,2)*0.5-ones(100,2); randn(100,2)*0.75];
Partition the training data into three clusters by using kmeans.
[idx,C] = kmeans(X,3);
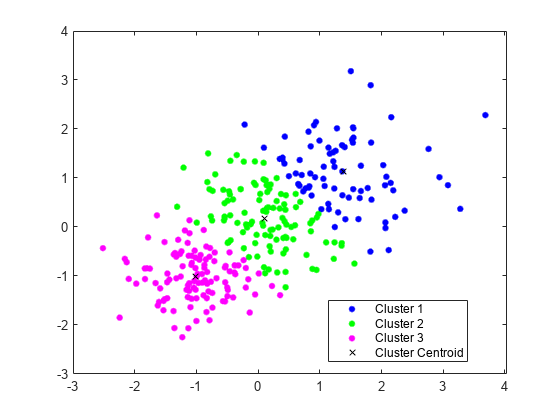
Plot the clusters and the cluster centroids.
figure gscatter(X(:,1),X(:,2),idx,'bgm') hold on plot(C(:,1),C(:,2),'kx') legend('Cluster 1','Cluster 2','Cluster 3','Cluster Centroid')
Assign New Data to Existing Clusters
Generate a test data set.
Xtest = [randn(10,2)*0.75+ones(10,2);
randn(10,2)*0.5-ones(10,2);
randn(10,2)*0.75];Classify the test data set using the existing clusters. Find the nearest centroid from each test data point by using pdist2.
[~,idx_test] = pdist2(C,Xtest,'euclidean','Smallest',1);
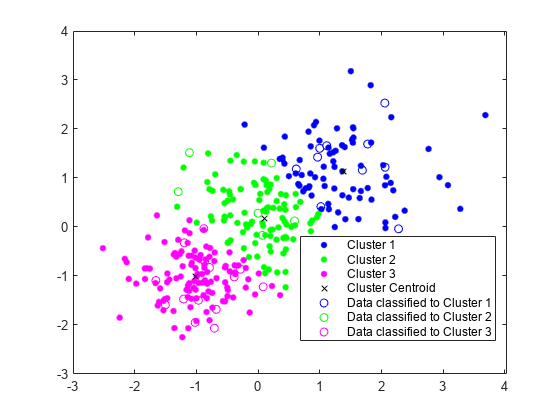
Plot the test data and label the test data using idx_test by using gscatter.
gscatter(Xtest(:,1),Xtest(:,2),idx_test,'bgm','ooo') legend('Cluster 1','Cluster 2','Cluster 3','Cluster Centroid', ... 'Data classified to Cluster 1','Data classified to Cluster 2', ... 'Data classified to Cluster 3')
Generate Code
Generate C code that assigns new data to the existing clusters. Note that generating C/C++ code requires MATLAB® Coder™.
Define an entry-point function named findNearestCentroid that accepts centroid positions and new data, and then find the nearest cluster by using pdist2.
Add the %#codegen compiler directive (or pragma) to the entry-point function after the function signature to indicate that you intend to generate code for the MATLAB algorithm. Adding this directive instructs the MATLAB Code Analyzer to help you diagnose and fix violations that would cause errors during code generation.
type findNearestCentroid % Display contents of findNearestCentroid.m
function idx = findNearestCentroid(C,X) %#codegen [~,idx] = pdist2(C,X,'euclidean','Smallest',1); % Find the nearest centroid
Note: If you click the button located in the upper-right section of this page and open this example in MATLAB®, then MATLAB® opens the example folder. This folder includes the entry-point function file.
Generate code by using codegen (MATLAB Coder). Because C and C++ are statically typed languages, you must determine the properties of all variables in the entry-point function at compile time. To specify the data type and array size of the inputs of findNearestCentroid, pass a MATLAB expression that represents the set of values with a certain data type and array size by using the -args option. For details, see Specify Variable-Size Arguments for Code Generation.
codegen findNearestCentroid -args {C,Xtest}
Code generation successful.
codegen generates the MEX function findNearestCentroid_mex with a platform-dependent extension.
Verify the generated code.
myIndx = findNearestCentroid(C,Xtest); myIndex_mex = findNearestCentroid_mex(C,Xtest); verifyMEX = isequal(idx_test,myIndx,myIndex_mex)
verifyMEX = logical
1
isequal returns logical 1 (true), which means all the inputs are equal. The comparison confirms that the pdist2 function, the findNearestCentroid function, and the MEX function return the same index.
You can also generate optimized CUDA® code using GPU Coder™.
cfg = coder.gpuConfig('mex'); codegen -config cfg findNearestCentroid -args {C,Xtest}
For more information on code generation, see General Code Generation Workflow. For more information on GPU coder, see Get Started with GPU Coder (GPU Coder) and Supported Functions (GPU Coder).
Input Arguments
X,Y — Input data
numeric matrix
Input data, specified as a numeric matrix. X is an
mx-by-n matrix and
Y is an
my-by-n matrix. Rows correspond to
individual observations, and columns correspond to individual
variables.
Data Types: single | double
Distance — Distance metric
character vector | string scalar | function handle
Distance metric, specified as a character vector, string scalar, or function handle, as described in the following table.
| Value | Description |
|---|---|
'euclidean' | Euclidean distance (default) |
'squaredeuclidean' | Squared Euclidean distance. (This option is provided for efficiency only. It does not satisfy the triangle inequality.) |
'seuclidean' | Standardized Euclidean distance. Each coordinate difference between observations is
scaled by dividing by the corresponding element of the standard deviation,
|
'fasteuclidean' | Euclidean distance computed by using an alternative algorithm that saves time
when the number of predictors is at least 10. In some cases, this faster
algorithm can reduce accuracy. Algorithms starting with
'fast' do not support sparse data. For details, see Algorithms. |
'fastsquaredeuclidean' | Squared Euclidean distance computed by using an alternative algorithm that
saves time when the number of predictors is at least 10. In some cases, this
faster algorithm can reduce accuracy. Algorithms starting with
'fast' do not support sparse data. For details, see Algorithms. |
'fastseuclidean' | Standardized Euclidean distance computed by using an alternative algorithm
that saves time when the number of predictors is at least 10. In some cases,
this faster algorithm can reduce accuracy. Algorithms starting with
'fast' do not support sparse data. For details, see Algorithms. |
'mahalanobis' | Mahalanobis distance, computed using the sample covariance of
|
'cityblock' | City block distance |
'minkowski' | Minkowski distance. The default exponent is 2. Use |
'chebychev' | Chebychev distance (maximum coordinate difference) |
'cosine' | One minus the cosine of the included angle between points (treated as vectors) |
'correlation' | One minus the sample correlation between points (treated as sequences of values) |
'hamming' | Hamming distance, which is the percentage of coordinates that differ |
'jaccard' | One minus the Jaccard coefficient, which is the percentage of nonzero coordinates that differ |
'spearman' | One minus the sample Spearman's rank correlation between observations (treated as sequences of values) |
@ | Custom distance function handle. A distance function has the form function D2 = distfun(ZI,ZJ) % calculation of distance ...
If your data is not sparse, you can generally compute distances more quickly by using a built-in distance metric instead of a function handle. |
For definitions, see Distance Metrics.
When you use 'seuclidean',
'minkowski', or 'mahalanobis', you
can specify an additional input argument DistParameter
to control these metrics. You can also use these metrics in the same way as
the other metrics with the default value of
DistParameter.
Example:
'minkowski'
Data Types: char | string | function_handle
DistParameter — Distance metric parameter values
positive scalar | numeric vector | numeric matrix
Distance metric parameter values, specified as a positive scalar, numeric vector, or
numeric matrix. This argument is valid only when you specify
Distance as 'seuclidean',
'minkowski', or 'mahalanobis'.
If
Distanceis'seuclidean',DistParameteris a vector of scaling factors for each dimension, specified as a positive vector. The default value isstd(X,'omitnan').If
Distanceis'minkowski',DistParameteris the exponent of Minkowski distance, specified as a positive scalar. The default value is 2.If
Distanceis'mahalanobis',DistParameteris a covariance matrix, specified as a numeric matrix. The default value iscov(X,'omitrows').DistParametermust be symmetric and positive definite.
Example:
'minkowski',3
Data Types: single | double
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: Either 'Smallest',K or 'Largest',K.
You cannot use both 'Smallest' and
'Largest'.
CacheSize — Size of Gram matrix in megabytes
1e3 (default) | positive scalar | 'maximal'
Size of the Gram matrix in megabytes, specified as a positive scalar
or 'maximal'. The pdist2
function can use CacheSize only when the
Distance argument begins with
fast.
If 'maximal', pdist2
attempts to allocate enough memory for an entire intermediate matrix
whose size is MX-by-MY, where
MX is the number of rows of the input data
X, and MY is the number of
rows of the input data Y. The cache size does not
have to be large enough for an entire intermediate matrix, but must be
at least large enough to hold an MX-by-1 vector.
Otherwise, pdist2 uses the regular algorithm
for computing Euclidean distance.
If the distance argument begins with fast and
CacheSize is too large or is
'maximal', pdist2 can
attempt to allocate a Gram matrix that exceeds the available memory. In
this case, MATLAB® issues an error.
Example: CacheSize='maximal'
Data Types: double | char | string
Smallest — Number of smallest distances to find
positive integer
Number of smallest distances to find, specified as the comma-separated
pair consisting of 'Smallest' and a positive integer.
If you specify 'Smallest', then
pdist2 sorts the distances in each column of
D in ascending order. You can use only one of
the arguments Smallest and
Largest.
Example: 'Smallest',3
Data Types: single | double
Largest — Number of largest distances to find
positive integer
Number of largest distances to find, specified as the comma-separated
pair consisting of 'Largest' and a positive integer.
If you specify 'Largest', then
pdist2 sorts the distances in each column of
D in descending order. You can use only one of
the arguments Smallest and
Largest.
Example: 'Largest',3
Data Types: single | double
Output Arguments
D — Pairwise distances
numeric matrix
Pairwise distances, returned as a numeric matrix.
If you do not specify either 'Smallest' or
'Largest', then D is an
mx-by-my matrix, where
mx and my are the number of
observations in X and Y,
respectively. D(i,j) is the distance between observation
i in X and observation
j in Y. If observation
i in X or observation
j in Y contains
NaN, then D(i,j) is
NaN for the built-in distance functions.
If you specify either 'Smallest' or
'Largest' as K, then
D is a
K-by-my matrix.
D contains either the K smallest
or K largest pairwise distances to observations in
X for each observation in Y.
For each observation in Y, pdist2
finds the K smallest or largest distances by computing
and comparing the distance values to all the observations in
X. If K is greater than
mx, pdist2 returns an
mx-by-my matrix.
More About
Distance Metrics
A distance metric is a function that defines a distance between
two observations. pdist2 supports various distance
metrics: Euclidean distance, standardized Euclidean distance, Mahalanobis distance,
city block distance, Minkowski distance, Chebychev distance, cosine distance,
correlation distance, Hamming distance, Jaccard distance, and Spearman
distance.
Given an mx-by-n data matrix X, which is treated as mx (1-by-n) row vectors x1, x2, ..., xmx, and an my-by-n data matrix Y, which is treated as my (1-by-n) row vectors y1, y2, ...,ymy, the various distances between the vector xs and yt are defined as follows:
Euclidean distance
The Euclidean distance is a special case of the Minkowski distance, where p = 2.
Specify Euclidean distance by setting the
Distanceparameter to'euclidean'.Standardized Euclidean distance
where V is the n-by-n diagonal matrix whose jth diagonal element is (S(j))2, where S is a vector of scaling factors for each dimension.
Specify standardized Euclidean distance by setting the
Distanceparameter to'seuclidean'.Fast Euclidean distance is the same as Euclidean distance, computed by using an alternative algorithm that saves time when the number of predictors is at least 10. In some cases, this faster algorithm can reduce accuracy. Does not support sparse data. See Fast Euclidean Distance Algorithm.
Specify fast Euclidean distance by setting the
Distanceparameter to'fasteuclidean'.Fast standardized Euclidean distance is the same as standardized Euclidean distance, computed by using an alternative algorithm that saves time when the number of predictors is at least 10. In some cases, this faster algorithm can reduce accuracy. Does not support sparse data. See Fast Euclidean Distance Algorithm.
Specify fast standardized Euclidean distance by setting the
Distanceparameter to'fastseuclidean'.Mahalanobis distance
where C is the covariance matrix.
Specify Mahalanobis distance by setting the
Distanceparameter to'mahalanobis'.City block distance
The city block distance is a special case of the Minkowski distance, where p = 1.
Specify city block distance by setting the
Distanceparameter to'cityblock'.Minkowski distance
For the special case of p = 1, the Minkowski distance gives the city block distance. For the special case of p = 2, the Minkowski distance gives the Euclidean distance. For the special case of p = ∞, the Minkowski distance gives the Chebychev distance.
Specify Minkowski distance by setting the
Distanceparameter to'minkowski'.Chebychev distance
The Chebychev distance is a special case of the Minkowski distance, where p = ∞.
Specify Chebychev distance by setting the
Distanceparameter to'chebychev'.Cosine distance
Specify cosine distance by setting the
Distanceparameter to'cosine'.Correlation distance
where
and
Specify correlation distance by setting the
Distanceparameter to'correlation'.Hamming distance is the percentage of coordinates that differ:
Specify Hamming distance by setting the
Distanceparameter to'hamming'.Jaccard distance is one minus the Jaccard coefficient, which is the percentage of nonzero coordinates that differ:
Specify Jaccard distance by setting the
Distanceparameter to'jaccard'.Spearman distance is one minus the sample Spearman's rank correlation between observations (treated as sequences of values):
where
Specify Spearman distance by setting the
Distanceparameter to'spearman'.
Algorithms
Fast Euclidean Distance Algorithm
The values of the Distance argument that begin fast
(such as 'fasteuclidean' and 'fastseuclidean')
calculate Euclidean distances using an algorithm that uses extra memory to save
computational time. This algorithm is named "Euclidean Distance Matrix Trick" in Albanie
[1] and elsewhere. Internal
testing shows that this algorithm saves time when the number of predictors is at least 10.
Algorithms starting with 'fast' do not support sparse data.
To find the matrix D of distances between all the points xi and xj, where each xi has n variables, the algorithm computes distance using the final line in the following equations:
The matrix in the last line of the equations is called the Gram matrix. Computing the set of squared distances is faster, but slightly less numerically stable, when you compute and use the Gram matrix instead of computing the squared distances by squaring and summing. For a discussion, see Albanie [1].
To store the Gram matrix, the software uses a cache with the default size of
1e3 megabytes. You can set the cache size using the
CacheSize name-value argument. If the value of
CacheSize is too large or "maximal",
pdist2 might try to allocate a Gram matrix that exceeds the
available memory. In this case, MATLAB issues an error.
References
[1] Albanie, Samuel. Euclidean Distance Matrix Trick. June, 2019. Available at https://www.robots.ox.ac.uk/%7Ealbanie/notes/Euclidean_distance_trick.pdf.
Extended Capabilities
Tall Arrays
Calculate with arrays that have more rows than fit in memory.
Usage notes and limitations:
The first input
Xmust be a tall array. InputYcannot be a tall array.
For more information, see Tall Arrays.
C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.
Usage notes and limitations:
The distance input argument value (
Distance) must be a compile-time constant. For example, to use the Minkowski distance, includecoder.Constant('Minkowski')in the-argsvalue ofcodegen.The distance input argument value (
Distance) cannot be a custom distance function.pdist2does not support code generation for fast Euclidean distance computations, meaning those distance metrics whose names begin withfast(for example,'fasteuclidean').Names in name-value arguments must be compile-time constants. For example, to use the
'Smallest'name-value pair argument in the generated code, include{coder.Constant('Smallest'),0}in the-argsvalue ofcodegen(MATLAB Coder).The sorted order of tied distances in the generated code can be different from the order in MATLAB due to numerical precision.
The generated code of
pdist2usesparfor(MATLAB Coder) to create loops that run in parallel on supported shared-memory multicore platforms in the generated code. If your compiler does not support the Open Multiprocessing (OpenMP) application interface or you disable OpenMP library, MATLAB Coder™ treats theparfor-loops asfor-loops. To find supported compilers, see Supported Compilers. To disable OpenMP library, set theEnableOpenMPproperty of the configuration object tofalse. For details, seecoder.CodeConfig(MATLAB Coder).pdist2returns integer-type (int32) indices in generated standalone C/C++ code. Therefore, the function allows for strict single-precision support when you use single-precision inputs. For MEX code generation, the function still returns double-precision indices to match the MATLAB behavior.Before R2020a:
pdist2returns double-precision indices in generated standalone C/C++ code.
For more information on code generation, see Introduction to Code Generation and General Code Generation Workflow.
GPU Code Generation
Generate CUDA® code for NVIDIA® GPUs using GPU Coder™.
Usage notes and limitations:
The supported distance input argument values (
Distance) for optimized CUDA code are'euclidean','squaredeuclidean','seuclidean','cityblock','minkowski','chebychev','cosine','correlation','hamming', and'jaccard'.Distancecannot be a custom distance function.Distancemust be a compile-time constant.Names in name-value pair arguments must be compile-time constants.
The sorted order of tied distances in the generated code can be different from the order in MATLAB due to numerical precision.
GPU Arrays
Accelerate code by running on a graphics processing unit (GPU) using Parallel Computing Toolbox™.
Usage notes and limitations:
You cannot specify the
Distanceinput argument as"fasteuclidean","fastsquaredeuclidean","fastseuclidean", or a custom distance function.
For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Version History
Introduced in R2010aR2023a: Fast Euclidean distance using a cache
The 'fasteuclidean', 'fastseuclidean', and
'fastsquaredeuclidean'
Distance metrics accelerate the computation of Euclidean
distances by using a cache and a different algorithm (see Algorithms). Set the size
of the cache using the CacheSize name-value argument.
See Also
pdist | createns | knnsearch | ExhaustiveSearcher | KDTreeSearcher
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)