fft
Fast Fourier transform
Description
Y = fft(X)X using a fast Fourier transform
(FFT) algorithm. Y is the same size as X.
If
Xis a vector, thenfft(X)returns the Fourier transform of the vector.If
Xis a matrix, thenfft(X)treats the columns ofXas vectors and returns the Fourier transform of each column.If
Xis a multidimensional array, thenfft(X)treats the values along the first array dimension whose size does not equal 1 as vectors and returns the Fourier transform of each vector.
Y = fft(X,n)n-point DFT.
If
Xis a vector and the length ofXis less thann, thenXis padded with trailing zeros to lengthn.If
Xis a vector and the length ofXis greater thann, thenXis truncated to lengthn.If
Xis a matrix, then each column is treated as in the vector case.If
Xis a multidimensional array, then the first array dimension whose size does not equal 1 is treated as in the vector case.
Examples
Input Arguments
Output Arguments
More About
Tips
The execution time of
fftdepends on the length of the transform. Transform lengths that have only small prime factors (not greater than 7) result in significantly faster execution time than those that are prime or have large prime factors.For most values of
n, real-input DFTs require roughly half the computation time of complex-input DFTs. However, whennhas large prime factors, there is little or no speed difference.You can potentially increase the speed of
fftusing the utility functionfftw. This function controls the optimization of the algorithm used to compute an FFT of a particular size and dimension.
Algorithms
The FFT functions (fft, fft2,
fftn, ifft, ifft2,
ifftn) are based on a library called FFTW [1]
[2].
References
[1] FFTW (https://www.fftw.org)
[2] Frigo, M., and S. G. Johnson. “FFTW: An Adaptive Software Architecture for the FFT.” Proceedings of the International Conference on Acoustics, Speech, and Signal Processing. Vol. 3, 1998, pp. 1381-1384.
Extended Capabilities
Version History
Introduced before R2006a

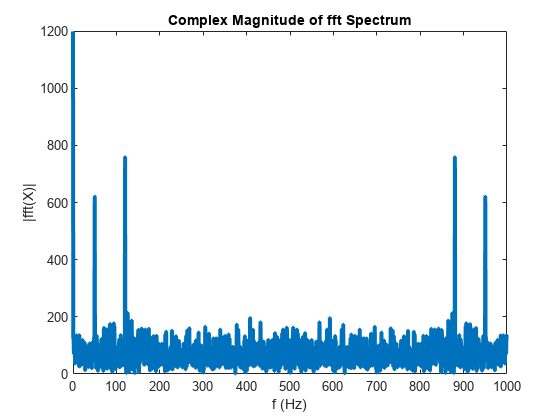
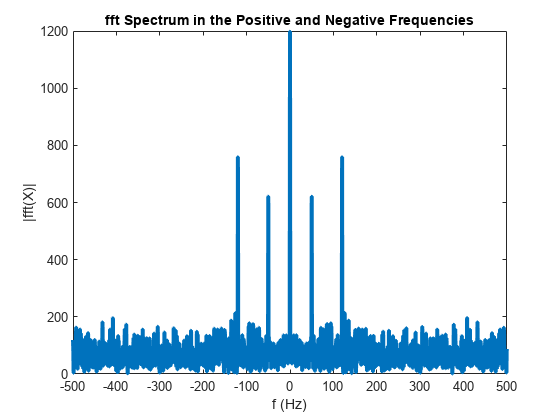
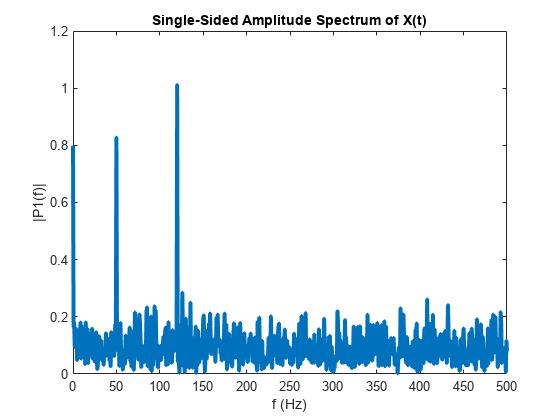
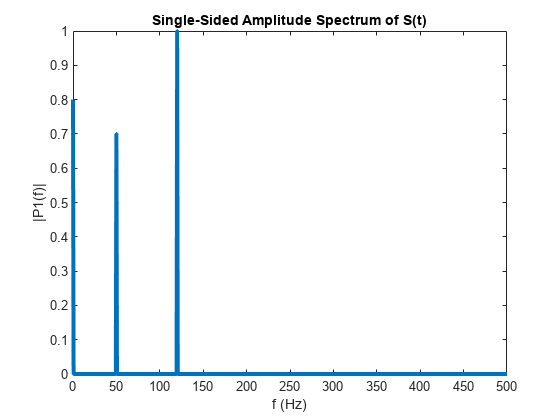
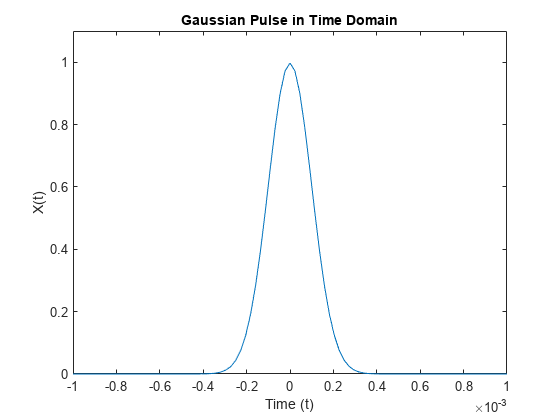
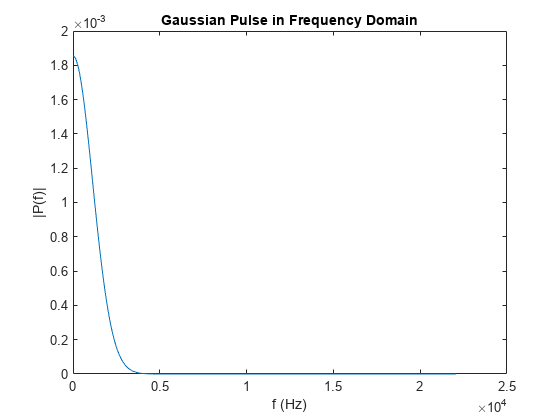
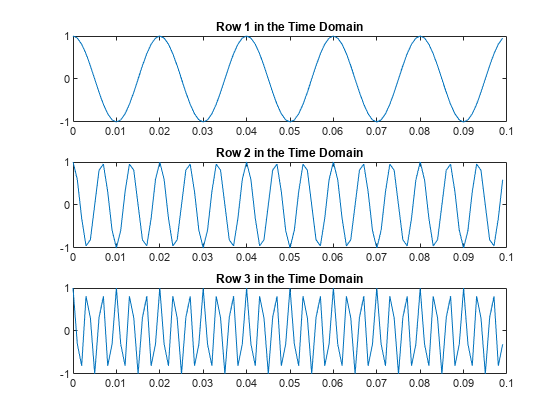
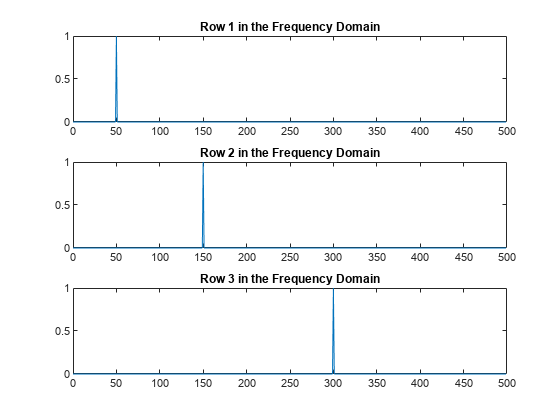
![fft(X,[],1) column-wise operation](fft_dim_1.png)
![fft(X,[],2) row-wise operation](fft_dim_2.png)
